Mining Sensor Data: Part 4

In “Mining sensor data” Part 1 and Part 2, we saw how mechanical systems generate vibration signatures that can indicate the health or ill health of a system.  In “Creating a Data Logger embedded application using the Intelligent Sensing Framework (ISF 2.1)“, Dave Munsinger demonstrated the software framework that we use to build embedded code for data logging applications.    More recently (Mining sensor data, Part3), Maureen Helm showed the framework we are using to build the windows-based clients that actually create the log files of interest.  My next post will followup on Maureen’s writeup.  But in this post, I want to again explore patterns in data.   I also want to show some mistakes that can be easily made.

When I first started looking at sensor data analytics, I explored techniques to predict defects in rotating machinery.  The techniques to do this are well known and documented, and there is an established industry that provides exactly this service.  I wanted to see if I could apply supervised machine learning techniques to the problem in an attempt to expand use of the techniques into other markets.  But over the course of the next few months, I learned a hard lesson:  Supervised machine learning requires data, lots of it.  I could (and did) attach sensors to lots of machinery to log “well behavior”.  The problem came when it came to logging “not-well behavior”.  Very few people were willing to let me run their motors to failure.  Those of you in the motor business have a ready supply.  I work for a semiconductor firm.  No such luck.

Figure 1: Data is everywhere

My boss (a very wise man) suggested that I change problems.  Why not look at kitchens?  Start simple: boil water.  Even I can boil water.  Boiling water makes noise, it vibrates.  And I can identify when water is NOT boiling, in a simmer state or in a rolling boil.  YEAH!  I can easily get known states for supervised learning!

I placed an accelerometer near a stock pot similar to that in Figure 1.  I also mounted one on the handle of the pot itself.  My data logger (which Maureen covered in the last post of this series) records raw data in .csv form, as well as metadata in XML format.  I was hoping to develop a simple model that could tell you the “state of the pot” based solely upon vibration data, so I used Matlab® to post-process a number of features from my accelerometer measurements:

• standard deviation
• variance
• kurtosis
• skew factor
• FFT coefficients
• range (max – min values)
• crossing rate (the percentage at which the signal crosses the mean value during a given period)
• cross-correlation between horizontal and vertical components of acceleration
• entropy of raw values
• entropy of some of the statistical measures above

Figure 2 below shows the standard deviation of the vector magnitude taken over several 30 second runs.  This looked pretty promising!

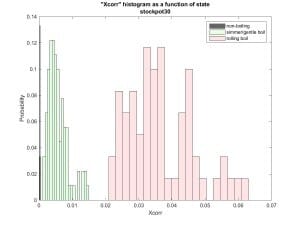
Figure 2: Standard deviation of the vector magnitude

Figure 3 shows the cross-correlation between the vertical and horizontal components of acceleration.  Still good!

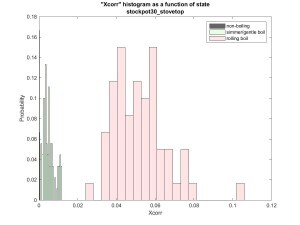
Figure 3: Cross correlation between vertical and horizontal vibrations

Crossing rates in Figure 4 aren’t bad either.

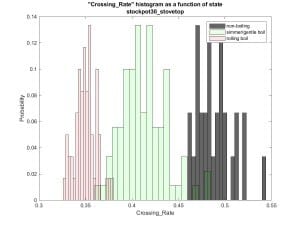
Figure 4: Crossing rates

Now if I were to plot these three by state, I can come up with a couple of planes in the three dimensional space that would appear to clearly differentiate non-boiling from simmer from rolling boil.

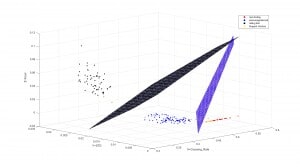
Figure 5: A 3-dimensional view

BUT NOT SO FAST!  For the data above, I treated the boiling process as if it had 3 distinct states.  In reality, it is a continuous process, which Figure 6 clearly demonstrates.  For that test sequence, I did a continuous log of data from cold all the way to rolling boil.

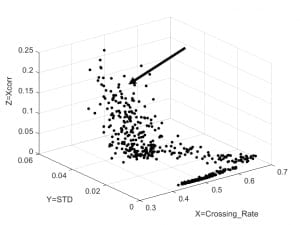
Figure 6: It’s really a continuous process

When I looked at Figure 6, I assumed that the area indicated by the arrow was associated with rolling boil.  BUT NOT SO FAST!

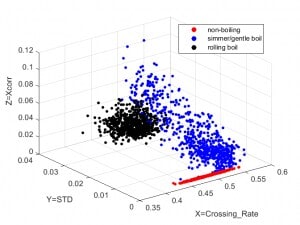
Figure 7: 10 minutes worth of data for each of 3 states

I went back to the kitchen and took three separate data sets, each over a 10 minute period of time and at each of my three desired states.  Figure 7 is the result.  Rolling boil data turned out to be nicely clustered, with much more variance in the simmer state.  What’s that all about?

Replotting the vector magnitude versus time for the dataset used in Figure 6, I got a really interesting result, shown in Figure 8 below.

Figure 8: Vector magnitude versus time

This looks almost exactly like a figure I later found in reference [1], labeled “Sound pressure signal of cooking process”.  Well, that makes sense.  I’m using an accelerometer to measure vibration, which is just another word for sound.  Another way to look at the data is by computing the standard deviation of a small window moving across the dataset of Figure 8.  This is shown in Figure 9, and you can clearly see a peak and subsequent decline to a stable value as the water goes into a rolling boil state.  I see similar shapes in plots for Power Spectral Density (PSD) log energy entropy, cross correlation, log energy entropy of the raw signal, variance and range feature types.

Figure 9: Standard deviation of the vector magnitude over time

To find out why, consult Figure 10, which I’ve borrowed from Wikipedia.  It plots rate of heat transfer versus the temperature of the pan above the saturation temperature T_s.  The downturn in Figures 8 and 9 corresponds to the “transition boiling” region of Figure 10.  In this area, we’re just starting to see a phenomenon known as “film boiling”.  When this starts to occur, our system becomes less efficient at transferring heat.  The curve levels out once film boiling dominates over nucleate boiling (which I’ve referred to as “simmer”).

Figure 10: Heat transfer for water ²

Great!  At this point we have data which matches known theory.  We should be ready to model our system. BUT NOT SO FAST! Just how repeatable is this?

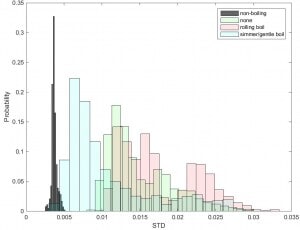
Figure 11: Standard deviation of the vector magnitude – Diversified!

State dependency in Figure 11 isn’t nearly so straight forward as we hoped in Figure 2.  Here I’ve included more datasets.  I’ve also included data from sensors located near other burners on the stove.  These are labeled “none” above, because there was no pot on the adjacent burner.  But in many cases, we still got vibration – from the pot across the stove!

Things are not so pretty any more.  Plots for cross correlation and crossing rates show similar overlap between states.

So what have we learned?

1. Don’t generalize from small sample sets.  Get lots of data.
2. Have you considered all variables that can affect your system? For the case above, what happens if we’re cooking soup, pasta or reducing cream?  What about stove type, size and number of burners, boil state, pot type, pot size, burner size, etc.  All of these must be recorded with your sensor data.
3. Although I didn’t mention it above, make sure you record the metadata for each run correctly.  Data entry errors in your logger form can be painful to correct later on.
4. Look at your data from lots of perspectives.  I refer to these as “features”.  Think standard deviation, crossing rates, entropy, etc.  Matlab is your friend when it comes to this kind of visualization.
5. Be sure you understand what your data is telling you.  The addition of state information to Figure 7 completely changed the way I was interpreting Figure 6.
6. Do not make assumptions on the form of your model.  I had hoped to take a vibration measurement, do some calculations and tell you which of three states the system was in.  But figures 8 and 9 clearly show that the same value on the Y axis can correspond to two different states.  That’s the same as saying we have overlapping states in the histogram of Figure 11.  To clearly differentiate between the three states, we’re going to have to introduce an assumption of continuous heating and time as a variable.
7. Consider how you are going to normalize your data.  For the problem above, you’ll see fairly dramatic changes in signal magnitudes as a function of pot shape, size and composition.   More water (mass) in the pot probably implies a better mechanical coupling to the stove, etc.
8. Make sure you can gather data for all expected states of the system.  Also make sure you gather data for cases of “interfering stimulus”.  In the case above, what if someone stirs the pot?  Or adds another pot to the stove top?
9. Research prior art.  There’s no need to reinvent the wheel.  Also, think about related areas.  When I dug into the topic of predicting boiling state from vibration data, I found relevant material dating back to the 1960s – for monitoring the state of cooling systems for nuclear reactors.

I’m not done with this problem just yet.  I am seeing some data signatures that should help me differentiate between burners on a stove top.  And I need to find the most robust method to identify the entry to the transition boiling region.  And don’t even ask me about spaghetti sauce!

Afterward

After submitting my initial draft of this post, I went back to a slightly revised version of Figures 8 and 9.  I then computed a moving average of the standard deviation.  The three are combined in Figure 12.

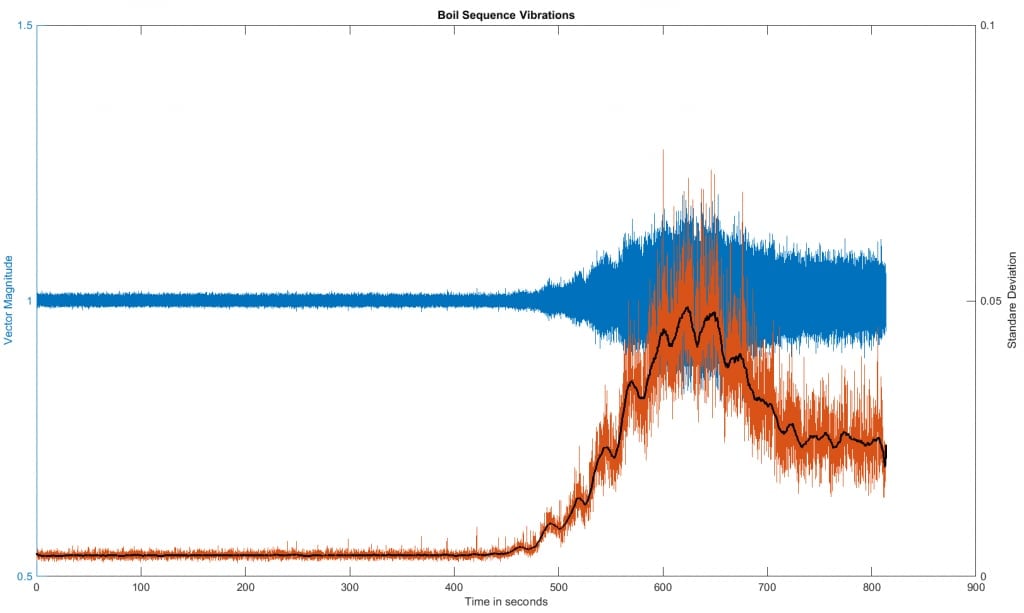
Figure 12: Raw data, standard deviation and moving average of the standard deviation

The black line is the moving average (100 samples) of the standard deviation (each in turn computed using 64 samples of the original data).  You might wonder about the cyclic signal that seems to be superimposed on it in the “simmer region”.  I did too.  Then I thought back and remembered that my stove cycled power to the burner on and off 2 to 3 times a minute during parts of my data collection.  That appears to correlate with what we are seeing here.  So just using a 3-axis accelerometer, we’ve been able to tease out when water starts to simmer, enters transition boiling, goes into full rolling boil, AND the cycling period of the stove it was heated on.