Our portable devices are getting more and more fun to use, due in part to new
generations of augmented and virtual reality applications. If you look at the
software source code at the heart of these AR and VR apps, you’ll
discover a common component: a mathematical model relating the position and
orientation of your portable device within an earth frame of reference. I
first touched on this back in my post
Degrees of freedom vs. axes. Now I want to dig into some of the ways to mathematically
model orientation. Perhaps the three most common are Euler angles, rotation
matrices and quaternions. Today’s discussion will focus on the Euler
angles and rotation matrices. We’ll follow up with quaternions in a
future posting.
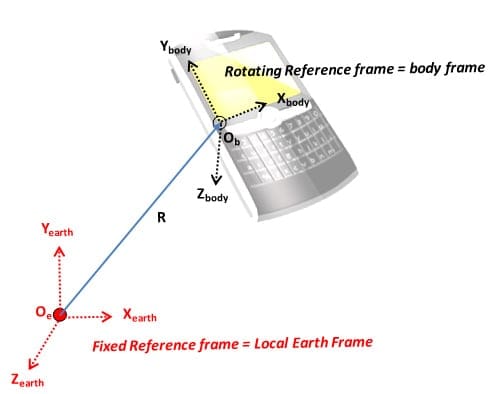
Figure 1: Local earth versus the body frame
The figure above is a variant of a figure that first showed up in
Accelerometer placement — where and why. Let’s arbitrarily choose the phone screen X,Y
coordinate system as our rotating frame of reference for this discussion. You
can intuitively see that any X,Y point (Z assumed zero) on the phone screen will
map to some X, Y, Z point in the earth frame of reference. It is also clear that
the Cartesian axes in the phone (or body) frame of reference will only rarely
align themselves with the local earth frame axes.
You probably first saw a figure like this in your high school geometry or trig
course. It allows us to map any point “A” in any standard X,Y
Cartesian system to any other X,Y Cartesian system, which is rotated from it by
some angle Psi (ψ), with a simple linear transformation. To see how,
let’s deconstruct that figure using a number of right triangles.
|
xe = xb cos(Y) – yb
sin(Y)
|
|
ye = xb sin(Y) + yb cos(Y)
|
| In matrix form: |
|
|
Aearth = C(-ψ) Abody
|
| The inverse of which is: |
|
|
Abody = C(ψ) Aearth
|
where Aearth and Abody are of the form [x y]T
and:
All other relationships included in this discussion can be similarly mapped to
a diagram of the rotation. The analysis also extends naturally to three
dimensions. If Aearth and Abody are of the form [x y
z]T
We will use the three dimensional form in the remainder of this discussion. In
both two and three dimensional cases, C(ψ) and C(-ψ) are known as
rotation matrices.
Notice that C(ψ) is the transpose of C(-ψ), and vice-versa:
C(ψ)T = C(-ψ). This is a special property of all
rotation matrices. You can reverse the sense of rotation simply by taking the
transpose of the original matrix.
Where I3×3 is simply the identity matrix:
This also implies that the inverse of a rotation matrix is simply its own
transpose:
Similar relationships hold for rotations in the X-Z (about the Y axis) plane:
|
xe = xb cos(θ) + zb
sin(θ)
|
|
ze = – xb sin(θ) + zb
cos(θ)
|
|
Aearth = C(-θ) Abody
|
|
Abody = C(θ) Aearth
|
|
ye = yb cos(Φ) – zb
sin(Φ)
|
|
ze = yb sin(Φ) + zb
cos(Φ)
|
|
Aearth = C(-Φ) Abody
|
|
Abody = C(Φ) Aearth
|
Phi, Theta and Psi (Φ, θ and ψ) rotations in sequence can
map a point in any right-hand-rule (RHR) 3-dimensional space into any other
RHR 3-dimensional space.
The composite rotation matrix is computed simply by multiplying the three
individual matrices in the specified order. Consistent with the discussion
above.
Collectively, Φ, θ and ψ are known as
Euler angles. You may also
see Φ, θ and ψ referred to as
“roll”, “pitch” and “yaw”
respectively. The subscript “RPY” in the expression above refers
to roll-pitch-yaw, and “YPR” refers to yaw-pitch-roll.
Euler angles are sometimes sub-divided into “Tait-Bryan” angles
(in which rotations occur about all three axes) and “Proper”
Euler angles (in which the first and third axes of rotation are the same).
Regardless of which type you use, it is important to specify the order of the
rotations — which IS significant. In the table below, the right-most
rotation is performed first, consistent with the matrix operations that will
be required to implement the rotation. Possible variants are:
| Alpha |
Angles |
Comments |
| YRP |
ψ-Φ-θ |
Tait-Bryan angles
(AKA Nautical or Cardan angles)
|
All of these are sometimes referred to simply as “Euler
Angles”
|
| YPR |
ψ-θ-Φ |
| PYR |
θ-ψ-Φ |
| PRY |
θ-Φ-ψ |
| RYP |
Φ-ψ-θ |
| RPY |
Φ-θ-ψ |
| RYR |
Φ-ψ-Φ |
Proper Euler Angles |
| RPR |
Φ-θ-Φ |
| PYP |
θ-ψ-θ |
| PRP |
θ-Φ-θ |
| YRY |
ψ-Φ-ψ |
| YPY |
ψ-θ-ψ |
A full discussion of Euler angles is beyond the scope of this article. But
some key points you need to take away are:
- Again, order of rotation matters!
-
There almost as many notations for Euler angles as the references in which
they appear. Be specific in your notation.
-
There may be multiple Euler angle combinations which map to the same
physical rotation. They are not unique.
-
There are typically limits on the range of Euler rotation for each axis (+/-
π or +/- π/2). These affect how the total rotation is spread
across the three angles. They also tend to introduce discontinuities when
Euler angles are computed over time.
-
Each Euler triad will map to 3×3 rotation matrix (which IS unique) in a
manner similar to that shown in Equations 24 and 25 above.
If you define a “reference orientation” for any object, then you
can define its current orientation as some rotation relative to that
reference. Tracking orientation over time is then equivalent to tracking
rotation from that reference over time. Because Euler angles are relatively
easy to visualize, they enjoyed early popularity in a number of fields. But
because of the shortcomings listed above, anyone who has used them extensively
invariably learns to despise them — I know I do!
Rotation matrices don’t require a master’s degree to be able to
use them. Anyone with a college freshman geometry class under their belt can
figure them out. They don’t have the ambiguities associated with Euler
angles, and can be found at the heart of many algorithms.





