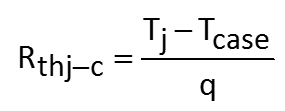If you’ve spent some time in the world of power semiconductors, then
it’s likely that you’ve come across the concept of
“thermal resistance.” If you haven’t come across this
before, or you need a refresher, then I’d recommend a look at the
Wikipedia
article or the
JEDEC
JESD51 series of standards, particularly JESD51-1, Section 2.
Thermal resistance can be thought of as a way to characterize the ease with
which heat energy travels through a particular pathway. There are several ways
of defining thermal resistance, and two of the most common are shown in Figure
1.
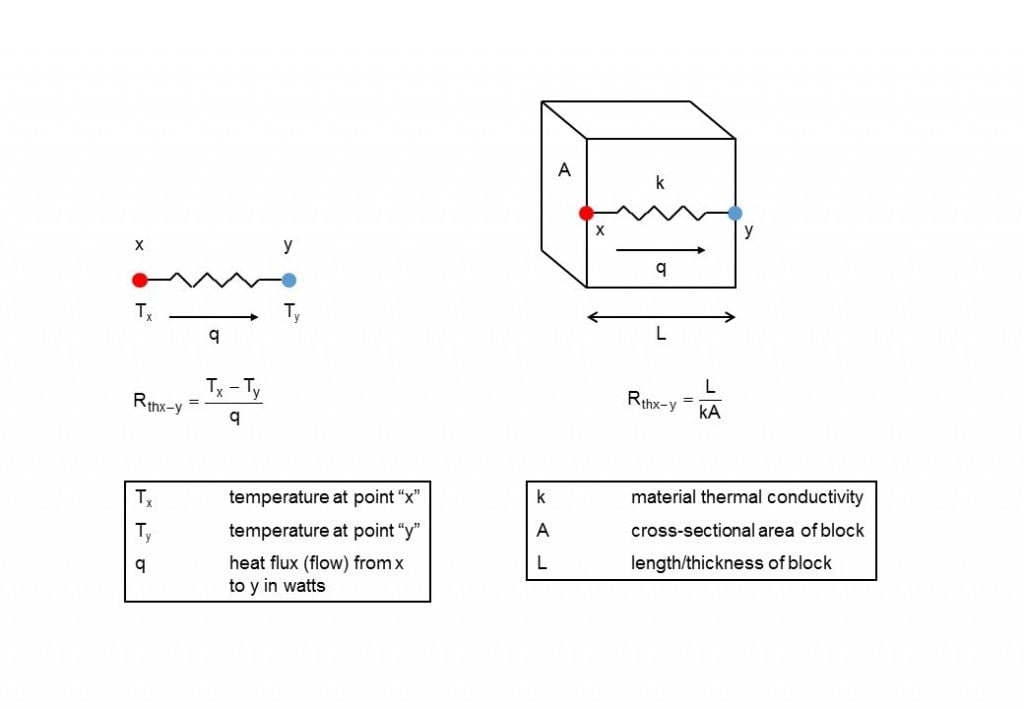
Figure 1 Thermal resistance defined in terms of temperature difference and
heat flux (left) and material dimensions and properties (right).
In Figure 1 (left) we are defining thermal resistance Rthx-y
[1]
simply in terms of the heat flow between two points at different temperatures,
without knowing anything about how the heat flows between those two points. In
Figure 1 (right), on the other hand, we define Rthx-y as a function
of the dimensions and thermal conductivity of a block of material, with the
assumption that heat flow is occurring through the mechanism of conduction
only. Note that in the right-side definition, we could also define Rthx-y
through a composite block of differing materials with different
“k” values simply by adding the thermal resistances of the
different layers together. Aha! So going back to our
original question, would a knowledge of the thermal resistance from the die to the top of the
case (Rthj-c) help us to determine Tj from
Tcase? See Figure 2.
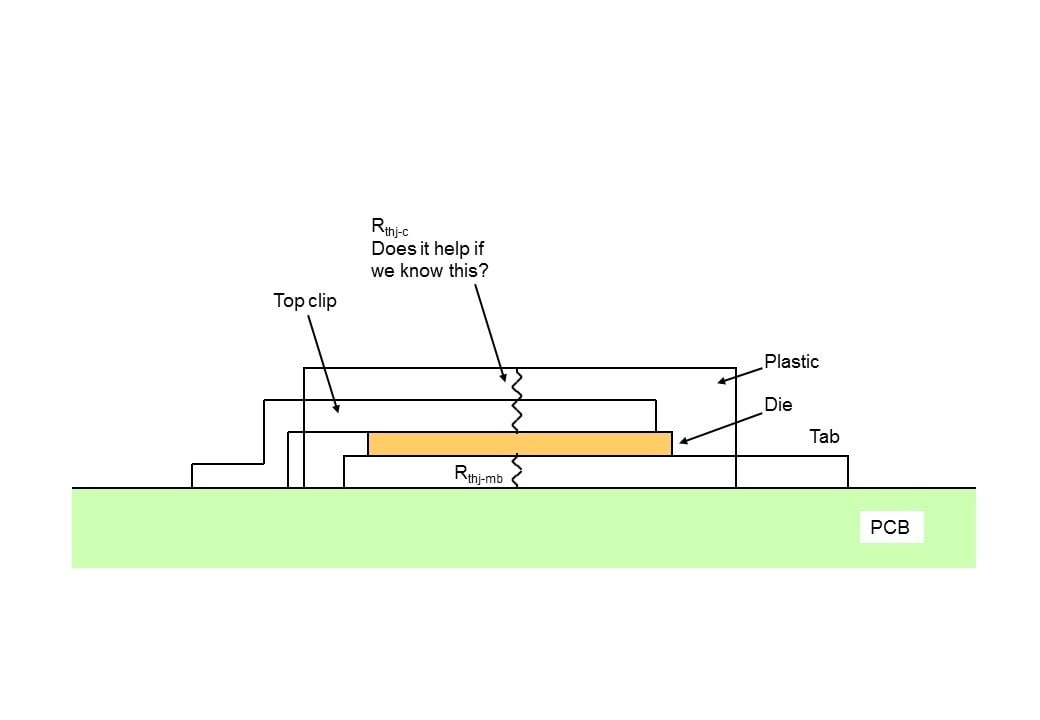
Figure 2 An idealized cross-section of an LFPAK MOSFET showing the location
of Rthj-c.
Rthj-c is the conduction-only thermal resistance from the die
through the top clip and plastic to the top surface of the device case,
although it is not one of our “standard” data sheet parameters.
So supposing our MOSFET supplier is kind enough to supply an Rthj-c
number, and we also have the equation
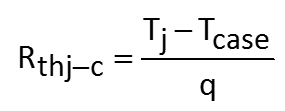
then we can find Tj from Tcase by a simple bit of
algebra, can’t we? Sadly, the answer is “no” for two very
good reasons:
First, re-arranging the above equation would give us

We’ve been given Rthj-c, and we can measure
Tcase, but what about the heat flux “q”? In other
words, what proportion of the total die dissipation is travelling upward
through the Rthj-c route? As far as I know, it is impossible to
measure this quantity under lab conditions. Attempts to estimate or calculate
a value for q is likely to lead to wildly inaccurate answers for
Tj. Although it superficially looks as if we can infer
Tj from Tcase using this method, it is of little or no
practical value.
Going back to the Figure 1 (left) definition of thermal resistance, the
second reason why attempting to use thermal resistances in this way is flawed.
The concept of thermal resistance assumes the heat energy flows down a
single, clearly defined path and the temperature at point “y” is
only dependent on that of point “x” and the heat flow q. It does
not consider any additional parallel paths from x to y – or that some
of the heat energy emanating from x may not even reach y at all! In
my previous
post, I demonstrated that the proportion of heat energy reaching the top of
the device case through the Rthj-c route is tiny. Furthermore, the
device is surrounded by air that has been warmed by heat loss from the
adjacent PCB surface.
The over-arching point I am trying to make is that thermal resistances are not
intended to be used as design tools. In fact, JEDEC makes this point
very clearly in JESD51-2:
“…The intent of (thermal resistance) measurements is solely for a thermal
performance comparison of one package to another in a standardized
environment. This methodology is not meant to and will not predict the
performance of a package in an application-specific environment.”
In my next post, I’ll explore a related theme: the usefulness (or
otherwise) of the concept of “top-side cooling.” In the
meantime, for an interesting and thought-provoking discussion of thermal
resistance, you might like to read
this article
by my former colleague Clemens Lasance.
[1]
Sometimes you may see Rth written as RΘ, mainly in American
texts. The two are interchangeable, but I’ll be sticking with
Rth.